martes, 12 de septiembre de 2017

SETIEMBRE - APOYO MATEMATICA

ENLACE PARA COMPLEMENTAR TEMAS TRATADOS EN CLASE:
Octubre



EJEMPLOS


LA ELIPSE -Teoría                                     Enlace video


Trazando una elipse en geogebra - video



PROPIEDADES DE LA MEDIATRIZ



 Actividad Elipse           Anexo 3 - Ficha de trabajo

Propósito:  
Ø  Construir una elipse e identificar sus elementos.
Ø  Determinar la ecuación de la elipse a partir de su  definición.
Ø  Graficar elipses a partir de su ecuación.
Integrantes:
·         __________________________________________________________________________
·         __________________________________________________________________________
Considerando la situación problemática que se presentó al inicio de la sesión, realiza las siguientes actividades:
Actividad 1
A. ¿Cómo explicarías la primera ley de Kepler con la imagen del anexo 1?
________________________________________________________________________________________________________________________________________________________
B. Considerando el anexo 2, ¿cuántos tipos de órbitas describen los satélites alrededor de la Tierra? ¿De qué depende dicha trayectoria?
________________________________________________________________________________________________________________________________________________________
Actividad 2: Dibuja en un plano cartesiano las elipses con coordenadas de los focos: (4;0) y      (-4:0). Utiliza una cuerda de diferente tamaño para cada caso (La cuerda tiene que ser mayor que la distancia focal)
Grupo N°1: longitud cuerda  L1                  Grupo N°2: longitud cuerda  L2 
Grupo N°3: longitud cuerda  L3                  Grupo N°4: longitud cuerda  L4 
Grupo N°5: longitud cuerda  L5 
Realiza los siguientes trazos en la elipse:
a.       El eje focal: recta que pasa por los focos “L” 
b.      Eje normal: recta que pasa por el centro y es perpendicular al eje focal B1B2
c.       Eje mayor: segmento que une a los vértices V1V2  de longitud 2a
d.      Eje menor: segmento que une B1B2 de longitud 2b.
e.      Anotan los elementos observados:    Coordenadas del centro:
Coordenadas de los vértices:                                             Distancia focal:

Actividad 3: Dibuja las elipses en un plano cartesiano utilizando una cuerda con longitud constante en cada uno de los casos: (sugerido 20cm).
Grupo N°1: Foco (3; -3) y ( 3;3)               Grupo N°2: Foco  -2; -2) y ( -2;2)
Grupo N°3: Foco (1;1) y (1;-3)                 Grupo N°4: Foco (-3;2) y (-3;4)
Grupo N°5: Foco (0; 5) y (0-5)
 Realizan los siguientes trazos en la elipse:
a)      El eje focal: recta que pasa por los focos “L”) 
b)      Eje normal: recta que pasa por el centro y es perpendicular al eje focal B1B2
c)       Eje mayor: segmento que une a los vértices V1V2  de longitud 2a
d)      Eje menor: segmento que une B1B2 de longitud 2b
e)      Anotan los elementos observados:
Coordenadas del centro:                Coordenadas de los vértices:             Distancia focal:

Ecuaciones de la circunferencia
Actividad:
Coordenadas en el patio o en geobegra
Los alumnos ubican el plano cartesiano, planteado en el patio o en geogebra, las coordenadas de los puntos y luego genera la circunferencia y su ecuaciòn respectiva:
P1 (8 ; 0 )  , P2 (5,6 ; 5,6 ) ,  P3 (0 ; 8 ) ,  P4 (-5,6 ; 5,6 ) , 
   P5 (-8 ; 0 ) , P6 (-5,6 ; -5,6 ) , P7 (0 ; -8 ) , P8 ( 5,6 ; -5,6 )

ÓRBITAS CIRCULARES Y ELÍPTICAS DE UBICACIÓN

1. Enlace al tema
Vídeo 


ÓRBITA GEOESTACIONARIA


 ECUACION DE LA CIRCUNFERENCIA
Haz doble clic en el siguiente texto:

Haz doble clic en el siguiente texto:

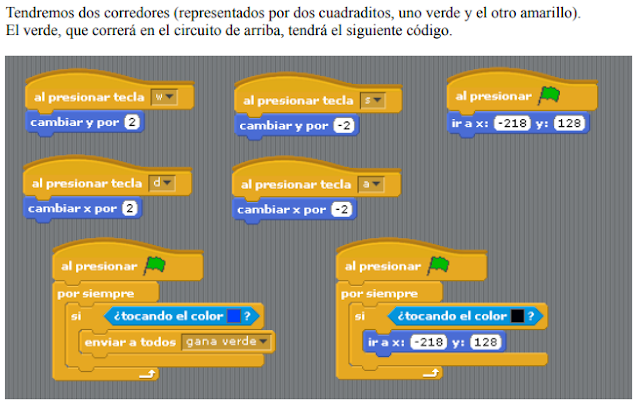
APOYO CON PROGRAMACIÒN EN SCRATCH
UBICANDO COORDENADAS:

LABERINTO




1ra  Semana Setiembre

I.E. JESÚS REDENTOR
AREA MATEMATICA                Apellido y nombre: ……………………………………….

Profesor Victor Morales Avila                  5to ………               02 / 09 / 2017

DISTANCIA - PENDIENTE- PUNTO MEDIO -

DESARROLLA LOS 12 CASOS
Puedes encontrar una guía en el siguiente url fuente
http://wolframalpha0.blogspot.pe/2012/02/distancia-punto-medio-pendiente.html
O haz clic en la siguiente texto: Tema a tratar

Graficar en el plano cartesiano y luego responde:
1.    La distancia entre los puntos A(-7,-2) y B(2,7) es:
2.    La pendiente entre los puntos A(-7,-2) y B(2,7)  es:
3.    Las coordenadas del punto medio entre los puntos A(-7,-2) y B(2,7)  es:


  



Graficar en el plano cartesiano y luego responde:
4.    La distancia entre los puntos P(8,-4) y Q(-9,7) es:
5.    La pendiente entre los puntos P(8,-4) y Q(-9,7) es:
6.    Las coordenadas del punto medio entre los puntos P(8,-4) y Q(-9,7) es:








Graficar en el plano cartesiano y luego responde:
7.    La distancia entre los puntos A(-2, 6) y B( 5, -8) es:
8.    La pendiente entre los puntos A(-2, 6) y B( 5, -8) es:
9.    Las coordenadas del punto medio entre los puntos A(-2, 6) y B( 5, -8) es:







Graficar en el plano cartesiano y luego responde:
10. La distancia entre los puntos P(1, 3) y Q( 4, -2) es:
11. La pendiente entre los puntos P(1, 3) y Q( 4, -2) es:
12. Las coordenadas del punto medio entre los puntos P(1, 3) y Q( 4, -2) es:



Estimados alumnos  no los estoy descuidando transitoriamente estoy usando este medio para continuar con nuestros temas, los cuales serán notas a tomar en cuenta            
Agosto
Semana del 14 al 18 
PUNTOS, RECTAS Y PENDIENTES EN EL PLANO CARTESIANO
Reponde las preguntas planteadas, luego de observar el vídeo;
1. En tu cuaderno grafica los puntos P(2;3) y Q (-1; -2) y luego une estos puntos con un segmento y prolonga la recta formada. Con tu transportador mide el ángulo de inclinación respecto a la horizontal . Anota esos datos.
2. En el tema distancia entre dos puntos, anota en tu cuaderno la distancia entre los puntos planteados en dicho ejemplo. 
  Marca tu respuesta respecto a la distancia entre los puntos: A)2  B)4  C)5
3. Como caso adicional grafica los puntos M (2;2) y N (7;14) luego calcula la distancia entre ellos.
Elige la respuesta respecto a la distancia entre los puntos:  A) 6   B) 13  C) 10
4, Calcula la pendiente del caso anterior.
5. Anota todo el caso planteado en la que se calcula  la ecuación de la recta, con los puntos P (5;4) y  (0;2).
6. Anota la fórmula y el caso planteado respecto a punto medio.
7. Anota el ejemplo planteado para calcular el baricentro de un triángulo formado con tres puntos  no colineales. (Este tema ya ha sido tratado anteriormente)
8. Toma nota de la ecuación de la circunferencia.
Video:



Semana del 07 al 11
REPASANDO PROGRESIONES
Toma nota de los 4 casos planteados en cada vídeo propuesto: 
 VIDEO 1      


 VIDEO 2

     


Este tema ya lo hemos tratado en clase:
EVIDENCIANDO PROGRESIONES
NUESTRA MASCOTA DEL DÍA DEL LOGROel


ELEMENTOS DE  TRIGONOMETRÍA
GRAFICANDO FUNCIONES :
APLICANDO GRAFICA DE FUNCIONES
REPASO
Ingresa al siguiente HIPERVÍNCULO :   TRIGONOMETRIA REPASO 

 ACTIVIDAD UTILIZANDO EL GNIÓMETRO

Ejercicios de apoyo con That quiz

 Ingresa al siguiente HIPERVÍNCULO :   
 TRIGONOMETRÍA CON EL THATQUIZ


 Proyecto  CONSTRUYENDO UN GNIOMETRO
   

CONSTRUCCIÓN DE UN TEODOLITO CASERO
En el caso planteado , si AC = 20m  ¿Cuánto mide la altura BC ?













Calculando la altura del mástil.
A una distancia de 18 metros del pie del mástil, con un ángulo de elevación de 16 grado se observó hacia la parte mas alta ¿qué altura tiene el mástil ?




CONO - TRONCO DE CONO - CILINDRO

PRACTICA INTERACTIVA

 Ingresa al hipervínculo  
Actividad en el educaplay
Tronco de cono- cono -cilindro

Analizando caso planteado 
Se tiene una copa cuyo diámetro mayor mide 2,4 cm y el radio menor 1 cm.
Su altura mide 2 cm ¿Con cuantas copas llenas con agua se podrá completar  una botella de 750 ml ?
EVIDENCIAS DE LA VERIFICACIÓN DEL CENTRO DE GRAVEDAD DE UN POLÍGONO A PARTIR DE LAS COORDENADAS DE SUS VÉRTICES














EVIDENCIAS


 Coordenadas de ubicación

 Utilizando el google map anota las coordenadas de las esquinas del colegio y luego calcula el área del terreno




TRABAJO COMPLEMENTARIO

APOYO CON TRABAJO VIRTUAL

INGRESA AL SIGUIENTE URL:  USO DEL GEOGEBRA
Reconoce las principales herramientas
                 1.   Representa las ecuaciones del siguiente sistema
3X + 2Y = 20
2X + 3Y = 20
                                                                                     Ec 1            Ec 2
      Luego interprete el punto de intersección                x    y           x   y  
                                                                                                             0  10          -2   8                                                                                                              2   7             1   6
                 2.   Ubica y luego une los puntos:
                         a)    A (-3 ; 1 )   B ( -1 ; 7 )   C ( 6; 3 )
                         b)   A ( 1; -3 )    B (-3 ; 5)     C ( 5 ; 7)
                         c)    A( 0 ; 0 )  B ( 30 ; 5 )  C ( 10 ; 15 )
                         d)   P (-2; 3)  Q ( 3 ; 3 )  R ( 4 ; 0 )  D ( -3 ; 0 )
  Pues usar  el  That Quiz
Pregunta opcional para analizar:


Este trabajo te sube puntos en la nota mas baja...
Pregunta opcional para analizar:

SISTEMA DE ECUACIONES

Método de Determinantes


  




La Importancia de las Matemáticas (Prezi)
Respuesta de las 4 preguntas del sistema de ecuaciones de 1er grado


















I.E. JESÚS REDENTOR
ÁREA MATEMÁTICA
Profesor Victor Morales Avila                    Grado: Quinto                                            

PLANIFICACIÓN DE LA SESIÓN DE APRENDIZAJE
UNIDAD 7
NÚMERO DE SESIÓN
5

20 y 21 set 2017
I. TÍTULO DE LA SESIÓN
Movimientos elípticos

II. APRENDIZAJES ESPERADOS
COMPETENCIA
CAPACIDADES
INDICADORES
ACTÚA Y PIENSA MATEMÁTICAMENTE EN SITUACIONES DE FORMA, MOVIMIENTO Y LOCALIZACIÓN.
Comunica y representa ideas matemáticas.
§ Describe los movimientos elípticos mediante modelos algebraicos en el plano cartesiano.
Elabora y usa estrategias.
§ Halla puntos de coordenadas en el plano cartesiano a partir de la ecuación  de la elipse.

III. SECUENCIA DIDÁCTICA
Inicio: (20 minutos)
·  El docente da la bienvenida a los estudiantes y les invitan que observen el video del siguiente enlace:
· 

Según Kepler, el Sistema Planetario Solar describe una trayectoria elíptica alrededor del Sol. 
¿Cómo será la trayectoria de un satélite alrededor de la Tierra?
¿El funcionamiento del GPS dependerá de su trayectoria?
¿Cómo podemos representar gráficamente la trayectoria de un satélite alrededor de la Tierra y –simultáneamente- la trayectoria de la Tierra alrededor del Sol?
¿Qué representación matemática tiene cada uno de los elementos de una elipse?
 Luego, promueve el diálogo en función a las preguntas:





·  Los estudiantes dialogan e intercambian opiniones al interior del grupo.
·  El docente hace referencia a las actividades en las cuales centrará su atención  para el logro de los a aprendizajes esperados:
-La descripción de la trayectoria elíptica del Sistema Planetario Solar y de los satélites alrededor de la Tierra.
-La representación gráfica de la elipse a partir de la ubicación de sus focos.
- La verificación de un conjunto de posibilidades para determinar la ecuación de la elipse que responde a las condiciones del problema.
-La representación en el plano cartesiano de puntos de la elipse a partir de su ecuación.
· 

o     Se organizan en grupos de trabajo.
o     Acuerdan una forma o estrategia para comunicar los resultados.
o     Se respetan los acuerdos y los tiempos estipulados para cada actividad garantizando un trabajo efectivo.
o     Se respetan las opiniones e intervenciones de los estudiantes y se fomentan los espacios de diálogos y reflexión.
El docente  plantea las siguientes pautas de trabajo que serán consensuadas con los estudiantes:
Desarrollo: (60 minutos)
·  Los estudiantes que observen la gráfica de la trayectoria de la Tierra alrededor del Sol (anexo 1) y la gráfica de la trayectoria de satélites alrededor de la Tierra (anexo 2). A continuación,  desarrollan la actividad 1 de la ficha de trabajo (anexo3); la cual consiste en responder las siguientes preguntas:
 





A. ¿Cómo explicarías la primera Ley de Kepler con la imagen del anexo 1?
B. Considerando el anexo 2, ¿cuántos tipos de órbitas describen los satélites alrededor de la Tierra? ¿De qué depende dicha trayectoria?
·  Los estudiantes responden en tarjetas y las ubican en la pizarra. Un estudiante de cada grupo sustenta su respuesta. El docente sistematiza la información.
·  Los estudiantes pasan a desarrollar la actividad 2 de la ficha de trabajo, la cual consiste en representar en un plano cartesiano la elipse con la ayuda de una cuerda y dos tachuelas. Según el gráfico:
 




https://www.youtube.com/watch?v=FW5zsN-QztY
·  El docente hace énfasis en que para cualquier posición, la suma de las distancias al foco no varía (la longitud de la cuerda se está manteniendo fija en la construcción).
Manteniendo  la distancia entre los focos constante:
·   Cada equipo de trabajo dibuja en un plano cartesiano las elipses con coordenadas de los focos: (4;0) y (-4:0)  Cada grupo utiliza una cuerda de diferente tamaño (la cuerda tiene que ser mayor que la distancia focal). Pueden trabajar en el patio y si se cuenta con el AIP con el geogebra.
Grupo N°1: longitud cuerda  L1 
Grupo N°2: longitud cuerda  L2 
Grupo N°3: longitud cuerda  L3 
Grupo N°4: longitud cuerda  L4 
Grupo N°5: longitud cuerda  L5 
·  Los estudiantes realizan los siguientes trazos en la elipse:
a)      El eje focal: recta que pasa por los focos “L” 
b)      Eje normal: recta que pasa por el centro y es perpendicular al eje focal B1B2
c)       Eje mayor: segmento que une a los vértices V1V2  de longitud 2a
d)      Eje menor: segmento que une B1B2 de longitud 2b)
e)      Anotan los elementos observados:
Coordenadas del centro:         Coordenadas de los vértices:     Distancia focal:



·  Los estudiantes desarrollan la actividad 3 de la ficha de trabajo, cada equipo de trabajo  dibuja las elipses en un plano cartesiano utilizando una cuerda con longitud constante en cada uno de los casos: (sugerido 20cm)
Grupo N°1: Foco ( 3; -3) y ( 3;3)
Grupo N°2: Foco ( -2; -2) y ( -2;2)
Grupo N°3: Foco (1;1) y (1;-3)
Grupo N°4: Foco (-3;2) y (-3;4)
Grupo N°5: Foco (0; 5) y (0-5)
·  Los estudiantes realizan los siguientes trazos en la elipse:
a.       El eje focal: recta que pasa por los focos “L” 
b.      Eje normal: recta que pasa por el centro y es perpendicular al eje focal B1B2
c.       Eje mayor: segmento que une a los vértices V1V2  de longitud 2a
d.      Eje menor: segmento que une B1B2 de longitud 2b
e.      Los estudiantes anotan los elementos observados:
Coordenadas del centro:
Coordenadas de los vértices:
Distancia focal:
·   Los estudiantes reflexionan a partir de la experiencia que,  para cualquiera que sea el punto
Cierre: (10 minutos)
· 

·         La propiedad fundamental de toda elipse es: La suma de las distancias a cualquier punto (x;y) hasta los focos es una constante.
·          Las órbitas de los planetas en el Sistema Solar son elípticas.
·         Cada circunferencia responde a una determinada ecuación matemática.
 El docente con la participación de los estudiantes llegan a las siguientes conclusiones:




·  El docente plantea algunas preguntas metacognitivas:
¿Qué aprendimos el día de hoy? ¿Cómo lo aprendimos? ¿De qué manera lo aprendido nos ayuda en nuestra vida cotidiana?

IV. TAREA A TRABAJAR EN CASA
·         El docente solicita a los estudiantes que resuelvan los problemas de las páginas 216 – 217 (Manual del docente).

V. MATERIALES O RECURSOS A UTILIZAR
Recursos para el docente:
-       Ministerio de Educación (2015). Rutas del Aprendizaje ciclo VII. Lima- Perú.




ANEXO N° 1
 


Anexo 1 - Sistema Planetario Solar
 
















Anexo 2 - Órbitas satelitales
















Según la distancia de la órbita al centro terrestre, las órbitas pueden clasificarse genéricamente como:
- De baja altitud (LEO, Low Earth Orbit). Para distancias entre 500 y 1.500 kilómetros. No pueden ser más bajas para evitar coberturas y pequeñas fricciones con la capa superior de la atmósfera. Tampoco pueden ser mayores para evitar el primer cinturón de radiación. Se usan constelaciones para cubrir el área de servicio.
- De media altitud (MEO, Medium Earth Orbit). Entre 6.000 y 11.000 kilómetros, entre el primer y el segundo cinturón de radiación; también existen en torno a los 20.000 kilómetros de altitud. Las órbitas MEO circulares se denominan ICO (Intermediate Circular Orbit).
-Órbita geoestacionaria (GEO, Geostationary Orbit). Situada a 35.788 kilómetros. En ella, el satélite gira solidariamente con la Tierra aparentando estar en un punto fijo.
-Altamente elípticas (HEO, High Elliptical Orbit). Cubren regiones alcanzables por GEO.




Anexo 3 - Ficha de trabajo
Propósito:  
Ø  Construir una elipse e identificar sus elementos.
Ø  Determinar la ecuación de la elipse a partir de su  definición.
Ø  Graficar elipses a partir de su ecuación.
Integrantes:
·         __________________________________________________________________________
·         __________________________________________________________________________
Considerando la situación problemática que se presentó al inicio de la sesión, realiza las siguientes actividades:
Actividad 1
A. ¿Cómo explicarías la primera ley de Kepler con la imagen del anexo 1?
________________________________________________________________________________________________________________________________________________________
B. Considerando el anexo 2, ¿cuántos tipos de órbitas describen los satélites alrededor de la Tierra? ¿De qué depende dicha trayectoria?
________________________________________________________________________________________________________________________________________________________
Actividad 2: Dibuja en un plano cartesiano las elipses con coordenadas de los focos: (4;0) y      (-4:0). Utiliza una cuerda de diferente tamaño para cada caso (La cuerda tiene que ser mayor que la distancia focal)
Grupo N°1: longitud cuerda  L1                  Grupo N°2: longitud cuerda  L2 
Grupo N°3: longitud cuerda  L3                  Grupo N°4: longitud cuerda  L4 
Grupo N°5: longitud cuerda  L5 
Realiza los siguientes trazos en la elipse:
a.       El eje focal: recta que pasa por los focos “L” 
b.      Eje normal: recta que pasa por el centro y es perpendicular al eje focal B1B2
c.       Eje mayor: segmento que une a los vértices V1V2  de longitud 2a
d.      Eje menor: segmento que une B1B2 de longitud 2b.
e.      Anotan los elementos observados:    Coordenadas del centro:
Coordenadas de los vértices:                                             Distancia focal:
 

Actividad 3: Dibuja las elipses en un plano cartesiano utilizando una cuerda con longitud constante en cada uno de los casos: (sugerido 20cm).
Grupo N°1: Foco (3; -3) y ( 3;3)               Grupo N°2: Foco  -2; -2) y ( -2;2)
Grupo N°3: Foco (1;1) y (1;-3)                 Grupo N°4: Foco (-3;2) y (-3;4)
Grupo N°5: Foco (0; 5) y (0-5)
 Realizan los siguientes trazos en la elipse:
a)      El eje focal: recta que pasa por los focos “L”) 
b)      Eje normal: recta que pasa por el centro y es perpendicular al eje focal B1B2
c)       Eje mayor: segmento que une a los vértices V1V2  de longitud 2a
d)      Eje menor: segmento que une B1B2 de longitud 2b
e)      Anotan los elementos observados:
Coordenadas del centro:                Coordenadas de los vértices:             Distancia focal:

Leer más »
Publicado por en No hay comentarios:
Suscribirse a: Entradas (Atom)